Por lo tanto, un triángulo tiene 3 ángulos interiores, 3 lados y 3 vértices.
Si está contenido en una superficie plana se denomina triángulo, o trígono, un nombre menos común para este tipo de polígonos. Si está contenido en una superficie esférica se denomina triángulo esférico. Representado, en cartografía, sobre la superficie terrestre, se llama triángulo geodésico.
Los puntos principales de una figura geométrica, como los vértices de un polígono, suelen ser designados por letras latinas mayúsculas: A, B, C, ...
Un triángulo se nombra entonces como cualquier otro polígono, nombrando sucesivamente sus vértices, por ejemplo ABC. En el caso del triángulo, los vértices pueden darse en cualquier orden, porque cualquiera de las 6 maneras posibles corresponde a un recorrido de su perímetro. Esto ya no es cierto para polígonos con más vértices.
Los lados del triángulo se denotan, como todos los segmentos, por sus extremos: AB, BC y AC, en nuestro ejemplo.
Para nombrar la longitud de un lado, por lo general se utiliza el nombre del vértice opuesto, convertido a minúscula latina: a para BC, b para AC, c para AB.
La notación general para el ángulo entre dos segmentos OP y OQ que comparten el extremo O es
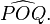
También podemos utilizar una letra minúscula, habitualmente griega, coronada por un acento circunflejo (en rigor, los ángulos deben ser designados por letras mayúsculas y su medida por minúsculas, pero a menudo se utilizan los mismos nombres para los dos con el fin de simplificar la notación). En el caso de un triángulo, el ángulo entre dos lados todavía puede, por tolerancia y en ausencia de ambigüedad, ser designado por el nombre del vértice común, coronado por un acento circunflejo. En resumen, en nuestro ejemplo, podemos observar los ángulos:
Un cuadrilátero es un polígono que tiene cuatro lados. Los cuadriláteros pueden tener distintas formas pero todos ellos tienen cuatro vértices y dos diagonales. Otros nombres usados para referirse a este polígono son tetrágono y cuadrángulo.
Los elementos de un cuadrilátero son:
- 4 vértices: los puntos de intersección de las rectas que conforman el cuadrilátero;
- 4 lados: los segmentos limitados por dos vértices contiguos;
- 2 diagonales: los segmentos cuyos extremos son dos vértices no contiguos;
- 4 ángulos interiores: conformados por dos lados y un vértice común;
- 4 ángulos exteriores: conformados por un lado, un vértice y la prolongación del lado ady.
Los ángulos interiores opuestos son iguales. Sus diagonales son perpendiculares entre si y cada una divide a la otra en partes iguales (esta característica por sí sola también define a los rombos).
Si un rombo es a la vez un rectángulo, entonces es un cuadrado. Un rombo con un ángulo interno de 45° suele llamarse losange.
Hay diversas maneras de calcular el área del rombo:
- El área del rombo es igual al producto entre dos lados y el seno del ángulo comprendido entre estos.
- El área del rombo es igual al semiproducto de sus diagonales (diagonal mayor y diagonal menor):
- Otra forma de hallar el área es a través del producto entre el semiperímetro y el radio del círculo inscrito en el rombo.

- siendo 2a es el semiperímetro del rombo; r el radio del circulo inscrito.
- El área también es igual al producto entre la base y la altura.
- siendo a la base; h la altura del rombo.



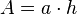
No hay comentarios:
Publicar un comentario